We’ve seen in the previous blog posts how Clojure’s persistent vectors work (if you’re interested, you can start at part 1). In part 3, we discovered how the persistent vector tail increases performance. However, in very performance critical code, this optimisation in itself is not enough: In many cases, this is because memory allocations are very resource consuming. You have to allocate memory, and the garbage collector might end up running more often. This is why Clojure’s transients were designed – to remove memory allocation overhead by allowing persistent data structures to be “mutable” within code that has to be efficient. They are not exactly the same as mutable data structures, although they are very similar.

The cool thing about transients is that they are not limited to persistent vectors. This concept can be used on more or less all persistent/immutable data structures that are directed acyclic graphs (DAG) – which is about all of them. Consequently, transients can also be used for persistent maps, sets, and RRB-trees.

When is it Ok to Mutate?

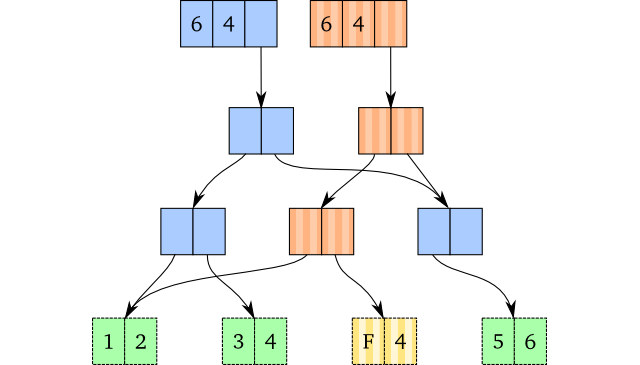
As a short recap, remember that modifications on a persistent vector do not mutate any existing nodes: Instead, we create new ones by the path copying algorithm. The image below visualises this, where the vertical striped persistent vector has copied the path down to element “3” and replaced it with an “F”.

Now, we want to mutate the node instead of copying it, but only when this doesn’t affect any other vector. So when will this be the case? It will be ok to mutate nodes if we know that the node is

1. only accessible by the original vector, and that
2. the original vector will never be used after this update ¹

This makes sense: As the old vector will not get used afterwards, it is okay to mutate the nodes only accessible by this vector!

Let’s assume the nonstriped vector in the image above will never be used after the update, and that all its nodes are only accessible by it. The leaf nodes (dashed edges) can be shared with other persistent vectors.

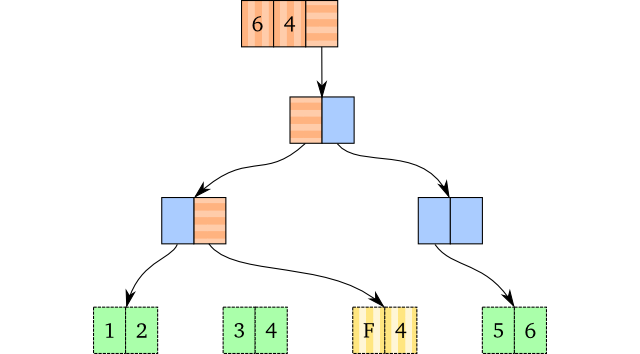
We can now mutate the nodes of that vector because it is safe to do so. The horizontally striped fields show the path we have taken, as well as the mutated fields. We cannot mutate the leaf node that contains “3” and “4” because it might be shared with other vectors. Instead, we copy it, as we would do in standard path copying. Of course, if we wanted to change “F” or “4” after this update and discard the old vector, we could mutate the leaf node too, as only this vector has access to it.

Since the old vector will not be used again, we don’t have to create a new vector head either. We just mutate the old vector head to avoid unnecessary memory allocations.

This sounds very easy, but we have to know that the nodes are only accessible by the original vector. We can separate this into two steps:

1. Check whether a node was created by the vector we’re mutating.
2. Ensure that no other vector has already been created out of this one.

Why is this sufficient? If the node we’re working was created when the vector was created, no previous vectors can refer to it. And if no other vectors have been created out of this one, then it is obvious that these nodes only are available to the vector itself.

Identification, Please

In order to find the nodes which this vector has created, we create a unique ID for each new vector and tag the nodes we copy/create with this ID. In this way, we know which nodes are created by the vector we’re operating on. If we additionally know that this vector satisfies 2. (No other vector created out of the original), we know that mutations are safe on this node. We will see how we can ensure 2. later, but for now, assume that 2. is true for this section.

Assuming we add IDs to every vector, including persistent ones, the original example with no mutation will look like the image below:

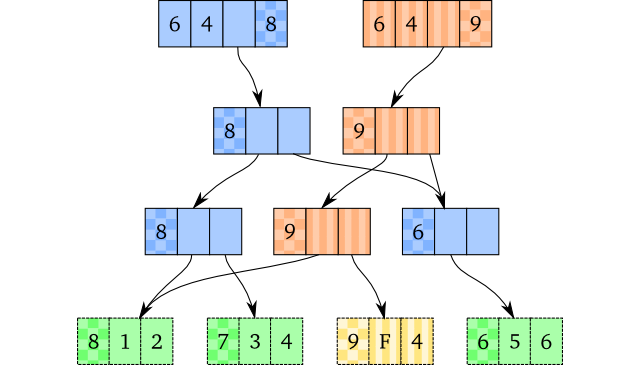
We use integers to represent IDs here for the sake of clarity, but note that any form of ID which guarantees uniqueness is totally fine. The new boxes – the checkered ones – contain the IDs of the vectors and nodes. Here, the original vector has ID 8 and the nodes with ID 8 were generated when that vector was created. The new vector has ID 9, and the nodes it had to create also has ID 9. The other nodes with different IDs, 6 and 7, are nodes from earlier versions of the vector with ID 8.

Now, let’s assume the vector with ID 8 will not be used afterwards, and that the next version of the vector will be the vector with ID 9 in the illustration above. It is then safe to mutate the nodes with ID 8. The mutated version will look like this:

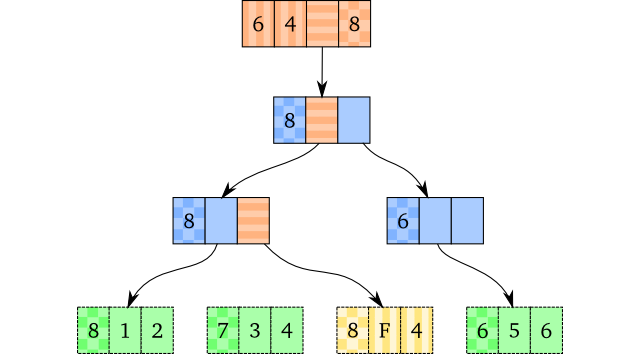
Notice that we also reuse the vector head and the ID. This is okay because the old vector is not going to be used afterwards.

Death on Updates!

Now, the IDs on nodes are easy to comprehend, and also easy to implement. The more difficult problem is how we ensure that no other vector has already been created. Additionally, we want to ensure that the transients aren’t used after they have been updated – otherwise, we could do a lookup on a value at different points in time and get different results, and that would be very bad.

You could imagine that a sufficiently smart compiler would detect when using the transient optimisations would be safe and when it wouldn’t. Unfortunately, there are several problems by only using that route. First, this requires a sufficiently smart compiler, and it is very likely impossible to ensure it catches all possibles cases where transients can be used. Second, the reason we wanted this optimisation in the first place, is because we wanted more performance in a particular part of the system we work on: This means we want some way of guaranteeing that the optimisation happens.

For this reason, to be able to use transient optimisations, you have to explicitly create a transient vector out of a persistent one. To do this in Clojure, you would have to use the transient function. Of course, the original persistent vector will not reflect the updates done on the transient – it is still immutable and will never change.

The way we ensure that aren’t used after they have been updated is now easy, we just say it is illegal to do anything to a transient after it has been updated. An update on a transient vector will invalidate it: That is, the moment we start a transient update, any operation (other updates, lookups) on the original vector will be invalid.

That’s all well and good, but how do we ensure that an updated transient isn’t used afterwards? If we create a new vector head, we’re wasting precious time on memory allocations. On the other hand, if we reuse the vector head, we cannot throw an error if the old transient was called. In Clojure, we currently have to trust that the programmer ensures that invalidated transients are NOT used. You could imagine ways to fix this through type checks in a statically typed language, but currently, there seems to be no implementation that fits transients perfectly².

All updates on a transient vector return a transient for performance, but it is also possible to convert the transient into a persistent vector. persistent! converts any transient back to a persistent vector in constant time, and invalidates it. We’ll have a look at how that is done now.

Creating Transients

Creating a transient out of a persistent vector is actually really easy: Just copy the vector head and create a new unique ID.

If the vector has a tail, we also copy it and increase it to its max size. Why? The tail is usually compact, appending a value to it would require us to copy the original one. For bulk insertions, that would mean a copy in 31 out of 32 appends, which is obviously not good. It’s much better to maximise the tail’s size and mutate it.

The vector heads below present the transient creation, and are 4-way branching to visualise tail expansion well. Note that they still have the same root. However, since the ID in the transient head differs from the ID in the root – 0 or null, in this case – the first update on the root itself will be a normal path copy update.

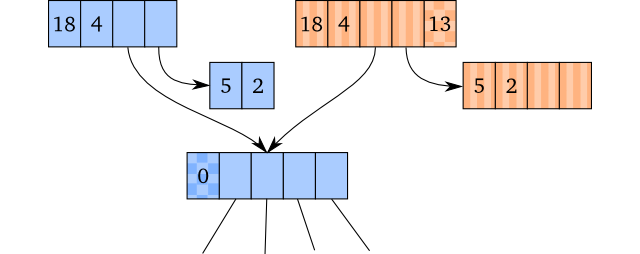
You can see that the original persistent vector head doesn’t contain any field for IDs at all. We can do that because the persistent vector implementation doesn’t really care about IDs. They may as well be null (or 0, as we use integers), and in fact, they are in the original persistent vector implementation. As long as the transients have a non-null ID, this is perfectly fine.

To sum it up, creating a transient require us to create a unique ID, a transient vector head and extending the tail. This is obviously a constant time operation (O(1)).

Now With More Complexity

The implementation in Clojure differs somewhat from what I just told you. However, it is based on the same idea, and it works more or less equivalently. Let’s see how it differs.

First, the ID is not stored in the vector head, it is instead stored in the root node of the vector. This means that the root node of the vector has to be copied as well.

Second, the ID is not an integer. Instead, it is an AtomicReference containing the thread ID, which is null for persistent vectors. So if we were to create a transient out of a persistent vector in Clojure, it will be more accurate to portray the illustration above like this:

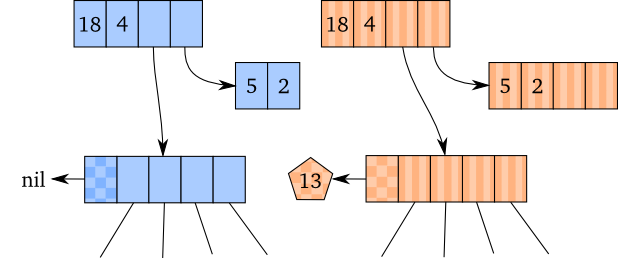
Why is this done in this fashion? The thread ID within the AtomicReference attempts to prevent erroneous usage by forcing transient usage to happen within a single thread. With version 1.7 of Clojure, this constraint is removed, and you can pass transients over to different threads and use them there if you want to.

I have no idea why the implementation copies the root node though – it doesn’t make much sense. I would guess that this is just legacy code which works, and as it works, there has been no need to change it.

From Transients to Persistent

Conversion back to a persistent vector is also not that complicated. We copy the vector head (sans the ID field) and compress the tail. In the original transient, we also set the ID to null (0). The result on a 4-way branching vector looks like this:

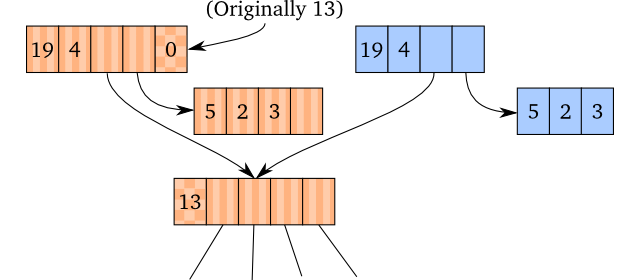
Copying the vector head and compressing the tail makes sense, but why is the ID field set to null in the transient? While we cannot ensure that the transient is used correctly while it’s updated, we know that the user cannot use the transient after it is converted to a persistent variant. We also know that persistent vectors use null as ID, so transients aren’t allowed to use null as an ID.

This means that any call when the transient’s ID is null is illegal because we know that it means that it has been converted to a persistent vector. Therefore, we can check the ID, and if it is null, we throw an exception.

As with the conversion from a persistent vector to a transient one, converting a transient back to a persistent version takes constant time (O(1)).

It’s All in the Details

Of course, what I told you above is also a bit different from the Clojure version. However, the same concept applies: We copy the vector head, compress the tail and set the ID to null. As the ID is stored in the vector root, we just set it to null there.

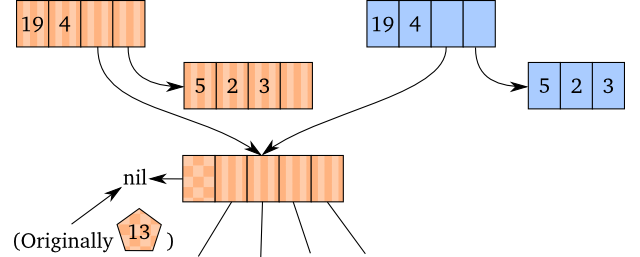
Given that you understood how the creation of a Clojure transient works, there should be no surprises here.

Mutable, but Still Not

Now if there is anything you should get out of this blog post, then it is that transients are not your standard mutable data structure. They might be perceived as such because their internals mutate, but they have a different API and acts differently.

And this is really important, because many people new to transients may believe they act like mutable data structures. They do not work like mutable data structures. The scary thing here is that it may look like they do. Just look at this piece of code:

(let [t (transient [])]
  (dotimes [i 10]
    (conj! t i))
  (persistent! t))
#_=> [0 1 2 3 4 5 6 7 8 9]

However, the transients provide no guarantee that they return the original head. In fact, the output above will likely not return the correct result when CLJ-1517 has been added to Clojure core.

This will also break in certain circumstances already. You can not find 8 8 and 9 9 in this map³, because this is not the correct way to use transients:

(let [t (transient {})]
  (dotimes [i 10]
    (assoc! t i i))
  (persistent! t))
#_=> {0 0, 1 1, 2 2, 3 3, 4 4, 5 5, 6 6, 7 7}

The correct way to do this is to pass the transient returned by assoc! to the next step, and use that one for the next assoc! call:

(persistent!
  (reduce (fn [t i] (assoc! t i i))
          (transient {})
          (range 10)))
#_=> {0 0, 7 7, 1 1, 4 4, 6 6, 3 3, 2 2, 9 9, 5 5, 8 8}

This sounds a bit inconvenient at first, until you realise that you only want to use transients where you originally used persistent vectors, and found them to be too inefficient. Suddenly this turns out to be really neat instead: Given that you adhere to the constraints, you can sort-of reason and think about them as persistent vectors. First, the API is identical, with the exception of update functions ending with !. Second, any query on the vector will always return the same answer, regardless of how many times you do it (given it is not invalidated). Third, any update function will return the new vector, not nil as mutable data structures do.

This means that – given you know the constraints are already kept – you can drop-in replace transients with persistent vectors. I have found this rare to happen in practice, but there is often surprisingly little work that has to be done due to the identical APIs.

Summary

Transients are an optimisation on persistent data structures, which decreases the number of memory allocations needed. This makes a huge difference in performance critical code.

One of the valuable things about them is that they have more or less the same API as the persistent ones. This means you can use the same lookup functions, and the same update functions if you append a “!” after it. Consequently, it is often not that hard to convert use of persistent data structures to transients in performance critical code. The only thing you have the be sure of is that you don’t use an updated transient.

Next Up

With this blog post, we’ve actually gone through all the parts required to implement a persistent vector in Clojure! Although an understanding of how it works is very valuable, we also need to know how efficient it is compared to other data structures, so the last part of this blog series will cover just that.