★ Understanding Clojure's Persistent Vectors, pt. 1
posted
You may or may not heard about Clojure’s persistent vectors. It is a data structure invented by Rich Hickey (influenced by Phil Bagwell’s paper on Ideal Hash Trees) for Clojure, which gives practically O(1) runtime for appends, updates, lookups and subvec. As they are persistent, every modification creates a new vector instead of changing the old one.
So, how do they work? I’ll try to explain them through a series of blogposts, in which we look at manageable parts each time. It will be a detailed explanation, with all the different oddities around the implementation as well.
For today, we’ll have a look at the basics and will cover updates, appends, and popping. The PersistentVector implementation in Clojure uses this as its core but also implements several speed optimisations, such transients and tails. We will have a look at those in later blog posts.
The Basic Idea
Mutable vectors and ArrayLists are generally just arrays which grow and shrink when needed. This works great when you want mutability, but is a big problem when you want persistence. You get slow modification operations because you’ll have to copy the whole array all the time, and it will use a lot of memory. It would be ideal to somehow avoid redundancy as much as possible without losing performance when looking up values, along with fast operations. That is exactly what Clojure’s persistent vector does, and it is done through balanced, ordered trees.
The idea is to implement a structure which is similar to a binary tree. The only difference is that the interior nodes in the tree have a reference to at most two subnodes, and does not contain any elements themselves. The leaf nodes contain at most two elements. The elements are in order, which means that the first element is the first element in the leftmost leaf, and the last element is the rightmost element in the rightmost leaf. For now, we require that all leaf nodes are at the same depth1. As an example, take a look at the tree below: It has the integers 0 to 8 in it, where 0 is the first element and 8 the last. The number 9 is the vector size:
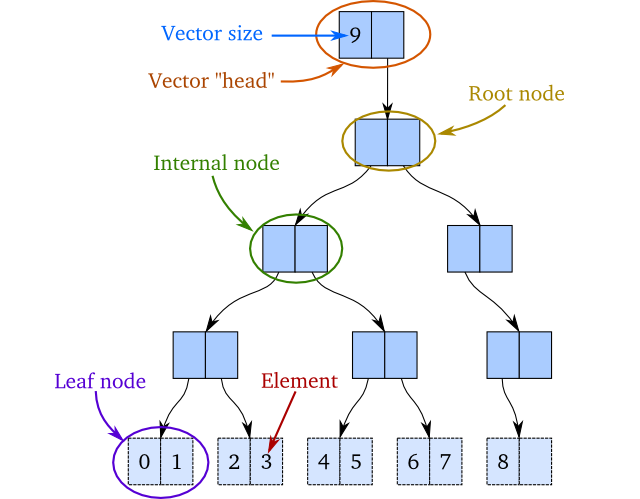
If we wanted to add a new element to the end of this vector and we were in the mutable world, we would insert 9 in the rightmost leaf node, like this:
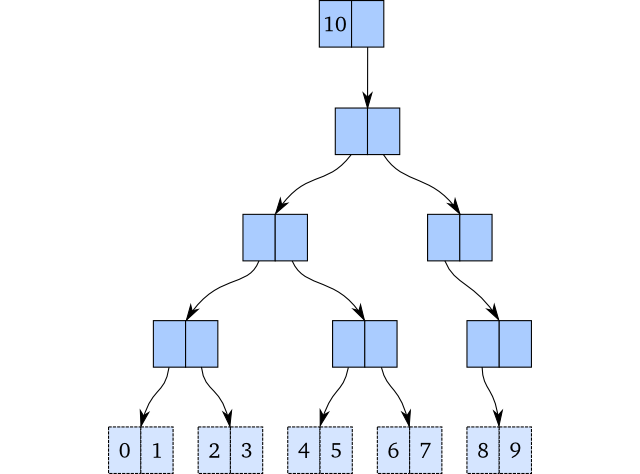
But here’s the issue: We cannot do that if we want to be persistent. And this would obviously not work if we wanted to update an element! We would need to copy the whole structure or at least parts of it.
To minimize copying while retaining full persistence, we perform path copying: We copy all nodes on the path down to the value we’re about to update or insert and replace the value with the new one when we’re at the bottom. A result of multiple insertions is shown below. Here, the vector with 7 elements share structure with a vector with 10 elements:
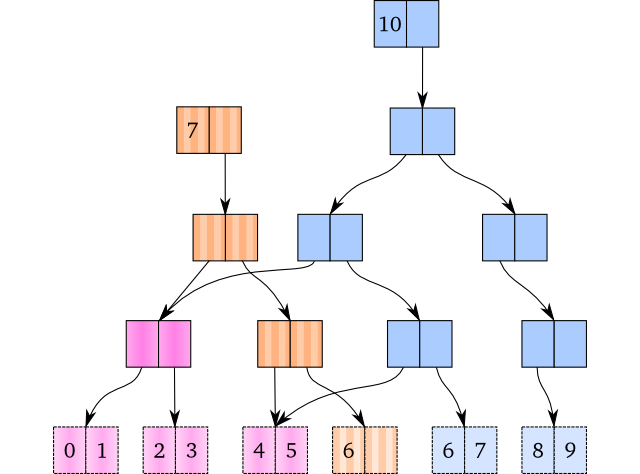
The pink coloured nodes are shared between the vectors, whereas the brown and blue are separate. Other vectors not visualized may also share nodes with these vectors.
Update
The easiest “modification” operator to understand would be updates/replacing
values in a vector, so we will explain how updating works first. In Clojure,
that’s an assoc modification, or an update-in/update.
To update an element, we would have to walk the tree down to the leaf node where the element is placed. While we walk down, we copy the nodes on our path to ensure persistence. When we’ve gotten down to the leaf node, we copy it and replace the value we wanted to replace with the new value. We then return the new vector with the modified path.
As an example, let’s assume we perform an assoc on the vector with the
elements from 0 to 8, like this:
(def brown [0 1 2 3 4 5 6 7 8])
(def blue (assoc brown 5 'beef))
The internal structures, where the blue vector has the copied path, is shown below:
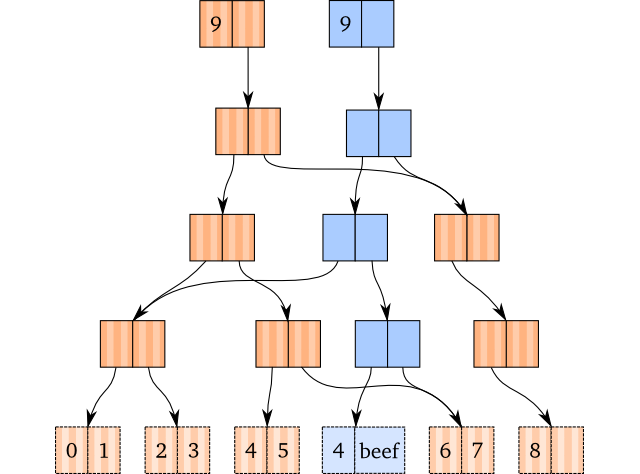
Given that we have a way to know which node to go down, this seems easy enough. (We’ll go through how we find the path to a specific index in the next part of this series.)
Appends
Appends (insertion at the end) are not too much different from updates, except that we have some edge cases where we have to generate nodes in order to fit in a value. Essentially, there are three cases:
- There is room for a new value in the rightmost leaf node.
- There is space in the root, but not in the rightmost leaf node.
- There is not enough space in the current root.
We’ll go through them all, as their solutions are not that difficult to grasp.
1: Just Like Assoc
Whenever there is enough space in the rightmost leaf node, we can just do as we do when we perform an assoc: We just copy the path, and at the newly created leaf node, we put in the value to the right of the rightmost element.
As an example, here’s how we would do (conj [0 1 2 3 4] 5), and the internal
structures from doing so. Blue is the new, brown is the old:
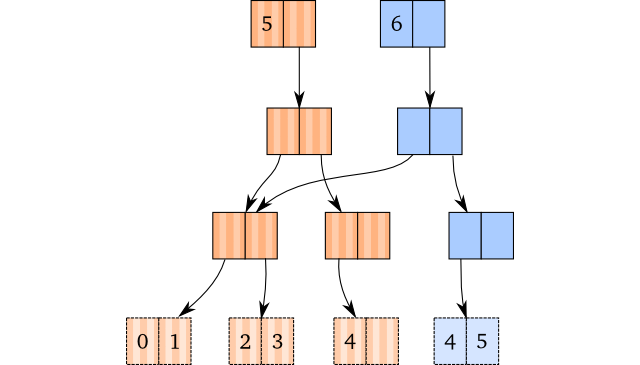
That’s it. There’s no magic, just path copying and insertion in the leaf node.
2: Generate Nodes When You Need Them
So, what do we do when there’s not enough space in the rightmost leaf node? Luckily, we’ll never end up in a position where we find out that we’re in the wrong leaf node: We will always take the right path down to the leaf node.
Instead, we will realize that the node we’re trying to go down to doesn’t yet
exist (the pointer is null). When a node doesn’t exist, we generate one
and set that one as the “copied” node.
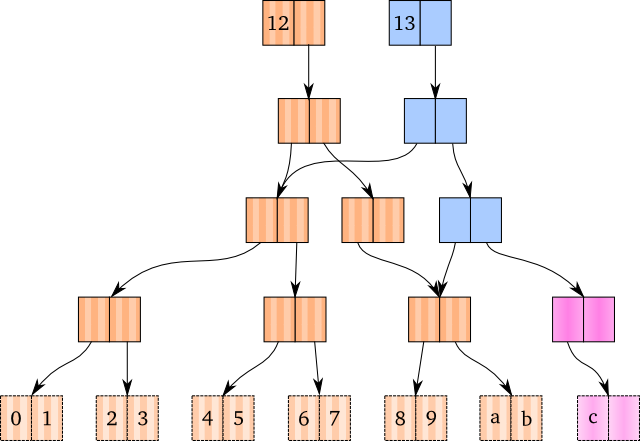
In the figure above, the pink nodes represent generated nodes. The blue nodes are nodes we’ve copied.
3: Root Overflow
The last case is the root overflow case. This happens when there isn’t more space in the tree with the current root node.
It’s not that difficult to understand how we would solve this: We make a new root node, and set the old root as the first child of the new root. From there on, we perform the node generating, just as we did in the previous solution. The example below shows the new root node as the purple node, and the generated nodes as pink ones.
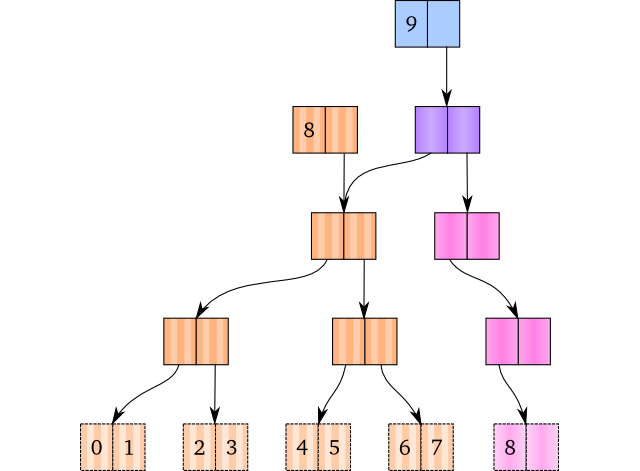
One thing is to solve the problem, but detecting when it happens is also important. Luckily, this is also rather easy. When we have a two-way branching vector, this happens when the old vector’s size is a power of two. Generally speaking, an n-way branching vector will overflow when its size is a power of n.
Popping
The solutions for popping (removing the last element) isn’t that difficult to grasp either. Popping is similar to appending in that there are three cases:
- The rightmost leaf node contains more than one element.
- The rightmost leaf node contains exactly one element (zero after popping).
- The root node contains exactly one element after popping.
Essentially, these are all ways of reverting 1, 2 and 3 in the previous section.
1: Dissoc to the Rescue
Again, we have a case where we can just do as we do when we update a structure: We copy the path down to the rightmost leaf node and remove the rightmost element in the copied leaf node. As long as there is at least one element left in the new leaf node, we don’t have to do any magic.
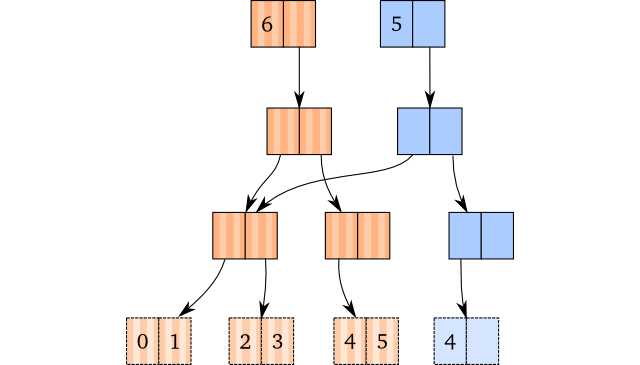
Keep in mind that popping multiple times on a vector will not yield identical vectors: They are equal, but they don’t share the root. For instance,
(def brown [0 1 2 3 4 5])
(def blue (pop brown))
(def green (pop brown))
will result in the following internal structure:
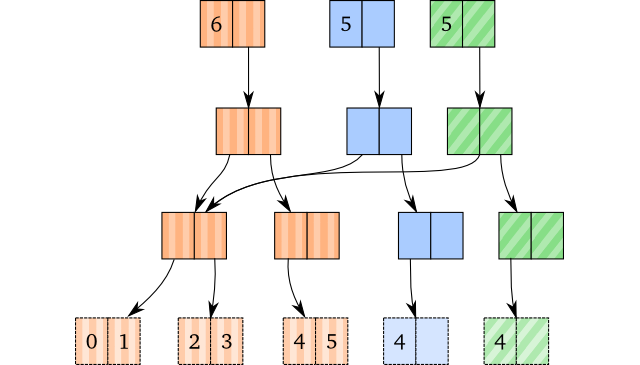
2: Removing Empty Nodes
Whenever we have a leaf node with only a single node, we have a different case.
We would like to avoid empty nodes in our tree at all cost. Therefore, whenever
we have an empty node, instead of returning it, we return null instead. The
parent node will then contain a null pointer, instead of a pointer to an empty
node:
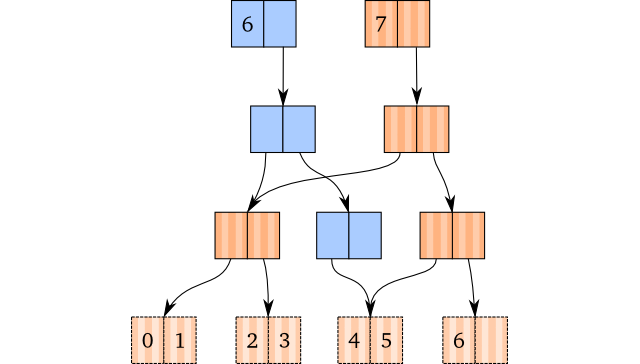
Here, the brown vector is the original, whereas the blue one is the popped one.
Unfortunately, it is not as easy as to just remove leaf nodes. You see, if we return a null pointer to a node, which originally only had one child, we must convert that one into a null pointer which we send back: The results of emptying a node propagates upwards. This is a bit tricky to get right, but essentially it works by looking at the new child, check if it is null and is supposed to be placed at index 0, and return null if that’s the case.
If this was implemented in Clojure, it may look something like this recursive function:
(defn node-pop [idx depth cur-node]
(let [sub-idx (calculate-subindex idx depth)]
(if (leaf-node? depth)
(if (== sub-idx 0)
nil
(copy-and-remove cur-node sub-idx))
; not leaf node
(let [child (node-pop idx (- depth 1)
(child-at cur-node sub-idx))]
(if (nil? child)
(if (== sub-idx 0)
nil
(copy-and-remove cur-node sub-idx))
(copy-and-replace cur-node sub-idx child))))))
When such a function has been implemented, node removal has been taken care of
completely. As an example, see the graph below. Here, the popped (blue) vector
has removed two nodes: The leaf node containing c and its parent.
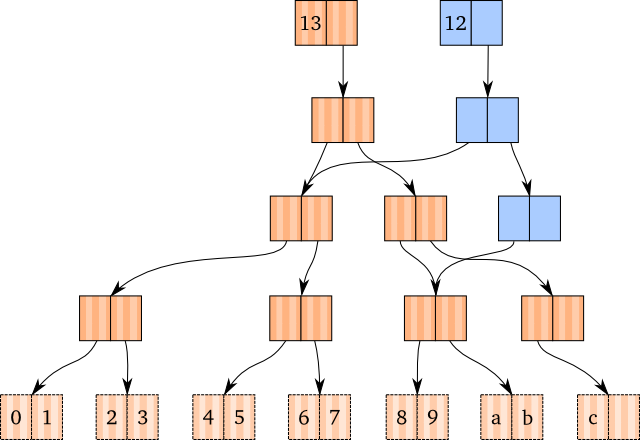
3: Root Killing
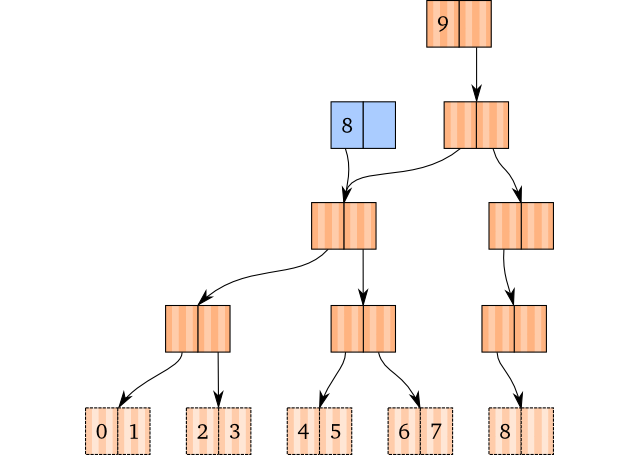
We have now covered all cases, except for one. With the current implementation, we would get the following result if we popped a vector with nine elements:
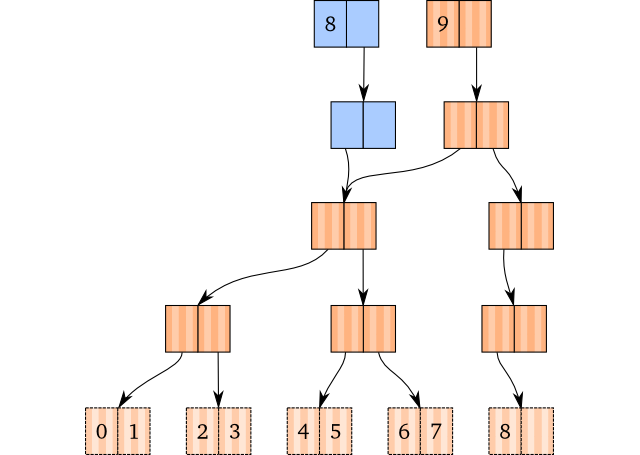
That’s right, we’d have a root with a single pointer to a child node. Pretty useless, as we would always move down into the child when we lookup or assoc values, and appending values would create a new root. What we would like to do is to get rid of it.
This is possibly the easiest thing in this blog post to actually do: After we have finished popping, check if the root node contains only a single child (check that the second child is null, for instance). If that’s the case, and the root node is not a leaf node, we can just replace the root node with its child.
The result is, as expected, a new vector (blue) with the first child of the original vector’s root node as root:
O(1) != O(log n)
Some people out there are probably wondering how this can be said to be O(1) at all. In fact, with only two children per node, this is O(log2 n), which is (relatively) far from O(1).
However, we don’t need to have only two children per node (often referred to as the branching factor). Clojure has 32 per node, which in result turns into very shallow trees. In fact, the trees will be at most 6 nodes deep if you have less than 1 billion elements in the vector. You need about 35 billion elements to get up to a depth of 8 nodes. At that point, I would believe memory consumption is a more serious issue.
To actually see the difference: Here is a 4-way branching tree with 14 elements, which only is 2 levels deep. If you scroll up a bit, you’ll see a figure with two vectors containing 13 and 12 elements, respectively. With two-way branching, this is already 4 levels deep, double the height as this one.
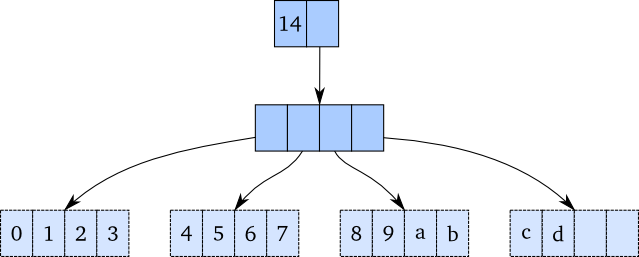
As a result of the incredibly shallow trees, we tend to call modifications and lookup of Clojure vectors to be “effectively” constant time, although they, in theory, are O(log32 n). People with basic knowledge in big O notation know that this is exactly the same as O(log n), but for marketing reasons, people like to add in the constant factor.
Next Up
Hopefully, this has given you better insight into how Clojure’s persistent vector works, and the general idea behind update, appends, and popping, along with an informal understanding on how they get their speed. Some optimizations on both appends and popping can be done, and I’ll blog about that after I’ve written about more “critical” parts of the vectors. In particular, the tail, how transients work, and how subvec work on the structure is of more relevance, and will thus come before tiny implementation details.
Part 2 of blog series talks about how one actually does the branching, and how we look up elements in details.
-
You can consider this as a simplification for the route picking, although it has some implications on the JVM speed due to the JVMs adaptive optimization. We’ll have a deeper look at this later on. ↩