Benchmarking algorithms is hard. A lot of things has to be considered, and a lot of things can go wrong. Fortunately, asymptotic analysis can give us a decent approximation before we get there. But, as hardware and algorithms grow more and more complex, the asymptotic analysis does as well.

We can use asymptotic analysis to approximate both time and memory usage, but especially time is very hard to get “right”. First, it’s not possible to get the wall-clock time through analysis. We’ve instead standardised on the number of CPU operations, which should at least give us a relative comparison on the same CPU. For example, for big values of \(n\), \(\mathcal{O}(1)\) is faster than \(\mathcal{O}(\log n)\).

At least that’s what we’ve been told. However, there are a lot of assumptions underneath the covers: Some are simply wrong, and in some situations, the standard \(\mathcal{O}\) notation just doesn’t cut it.

Array Lookup

To begin, let’s start with an operation we all are familiar with: Array lookups. If we ask the Internet, for example the Big-O Cheat Sheet, we see that access is \(\mathcal{O}(1)\).

Which is true given the right context. But without any assumptions, it’s not constant: If we look up index i in an n-length array, then we cannot do better than \(\mathcal{O}(\log i)\).

To see why, let’s begin with an example: Imagine I want to look up element 4,032,643,364,149,915,392,614,468,916 in an array. If we want to represent this number and all the ones below it, we need at least 92 bits. This is way more than the usual 32- or 64-bit numbers we use day to day.

If I continue to grow this number, the index itself will consume more and more memory. And regardless of how efficient we are at doing computations, we cannot process a variable number of bits in constant time. We are very good at processing up to 64 bits together, but when we go above this size, we currently need more CPU cycles to process the index itself.

Now, this makes sense, but it feels sort of silly. We don’t have machines (yet) with enough RAM to store an array with more than 2⁶⁴ elements, so could we not make the integer processing part a constant?

And this is exactly what we do: For all intents and purposes, we consider integer operations to take constant time. Formally, people say that they use the RAM Model of Computation (it also includes some other assumptions we’ll look at shortly).

So why do we do that? Even though it’s “wrong”, for real life input sizes it is not. And removing the factor helps us focus on the things that actually differs. If we didn’t, we’d have to write \(\log i\) all over the place!

Now, there are algorithms where we do have to consider integer operations as \(\mathcal{O}(\log i)\). But those are few and far between, and it’s usually mentioned or obvious that the integers grow that large.

Random Access

With our assumption that integer operations take constant time, surely an array lookup is \(\mathcal{O}(1)\), right? Actually no, and we can see this on machines if we perform repeated uniform random accesses on a big array:

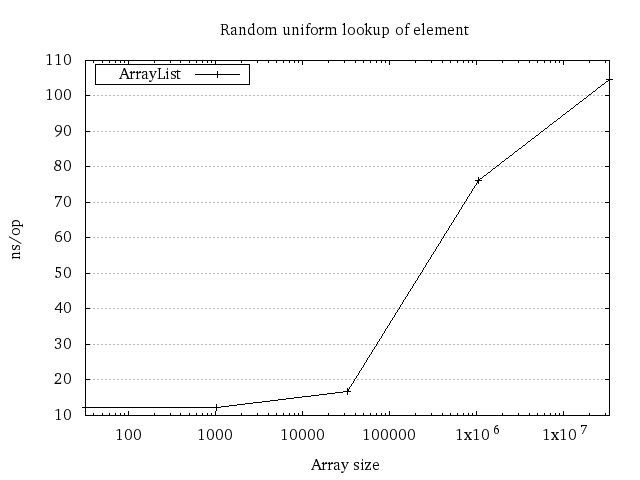
The reason it’s not constant has to do with random access and all the memory caches we have in our machine. With not much data, we can fit the entire dataset in the smaller caches. But when the size grows, the data will be distributed over the caches and RAM. Performing uniform random lookups will have a higher and higher chance of hitting a slower cache or RAM itself, making the calls slower and slower.

The RAM model of computation considers memory access to take constant time. This is wrong, even in real-world scenarios. Even so, it is usually fine for algorithms and is typically a bigger deal for data structures. It’s not without reason that databases use B-trees instead of binary trees for data!

When the RAM model is too coarse, there are two other memory models that may be used instead: The external memory model and the cache-oblivious model. Both assume that the memory hierarchy can be simplified down to this:

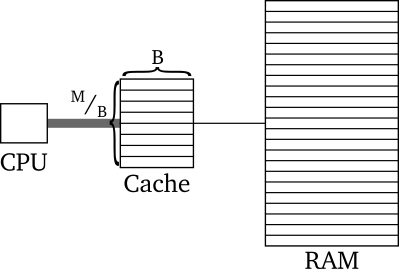
In these models, we assume that the cache lines have \(B\) bytes in them and that there is in total \(M\) memory in the cache (it follows that there are \(^M/_B\) cache lines in the cache). Both models assume that the major time cost is the transfer from Cache to RAM and vice versa. The Cache represents the cache closest to RAM, as moving data from RAM to cache is what will dominate the time consumption.

The external memory model assumes we know \(M\) and \(B\) and can optimise for those, and that we ourselves can evict the cache lines. In contrast, the cache oblivious model assumes that \(M\) and \(B\) are unknown. This means we have to optimise for all \(M\) and \(B\)¹.

These models help a lot, but they are not perfect. On most machines, a lot of programs are running concurrently, all fighting for the same resources, caches included. And if you’re running in the cloud, your virtual machine is likely to fight for the CPU cache with other VMs.

Array Appends

Sometimes, the models are good approximations. But sometimes, they measure only a small piece of your algorithm. And as Zach Tellman once said in a presentation

Performance is almost never the sum of its parts.

A great example of how this can lead people astray is through an analysis of dynamic arrays. Most – if not all – dynamically growing arrays are designed to support efficient insertion of elements at the end. Typically this is done by making a static array of size capacity, then use that for storing data. Then, if you want to append, there are two cases that could happen:

1. There’s enough space, and you put it in the next free slot
2. There’s not enough space, and you reallocate the array to make it bigger

Typically the new capacity set is 1.5 or double the previous capacity.

Because we need to consider the worst case scenario, the running time for an append is \(\mathcal{O}(n)\), where n is the size of the dynamic array. We will see case 1. much more frequently, and that one takes only \(\mathcal{O}(1)\) time. But because Big O notation by default must assume that a single algorithm call is done in isolation, we can’t do any better!

This is annoying, so computer scientists found a way to make this result more precise through what we call amortisation. Instead of considering a single operation in isolation, an amortised running time considers the total running time of \(m\) operations.

For dynamic arrays of size \(n\), if we double its size (\(m = n\)) by appending elements to it, we can show that its running time would take \(\mathcal{O}(n)\) in total. As such, we can say that the total running time per operation is “on average” \(\mathcal{O}(1)\).

Even though we say that the running time is \(\mathcal{O}(1)\), we have to qualify that this is an amortised running time. Some critical real-time systems cannot afford to wait for a single operation to take \(\mathcal{O}(n)\) time. It would be really bad if pacemakers all over the world started to skip a beat every now and then because somebody didn’t qualify that their algorithm was amortised!

Quicksort

While amortised time can be considered the average running time for \(m\) operations run in sequence, there are other averages out there as well. Quicksort is a great example of this. Its worst-case running time is \(\mathcal{O}(n^2)\), hardly anything to celebrate.

But in the same spirit as amortisation, it doesn’t represent the running time for an average run: If you were to take all the \(n!\) different permutations of the numbers 1 to \(n\), made them into lists, then sorted them all with quicksort, the total time used for sorting will be \(\mathcal{O}(n! n \log n)\), which is \(\mathcal{O}(n \log n)\) per permutation.

This means that the probability of actually hitting a case where you end up with \(\mathcal{O}(n^2)\) is very low! It’s there, but chances are you will not see this very often.

As with all assumptions, one has to know where they are wrong. Attackers can abuse this through algorithmic complexity attacks, which forces your system to waste time on carefully constructed pathological cases over and over again.

Summary

Asymptotic analysis is extremely valuable, but as with all abstractions, it is leaky. Even when you take into account that constant factors may shake things up for small \(n\)’s, assumptions about the memory model may be wrong. Or, although the analysis is correct for a single operation, it may not be correct for a collection of them.