We programmers tend to consume collections of data all the time. These days, when we have to talk to other systems to fetch it, the data is usually received through a JSON HTTP API or a connection to a SQL database. What you quickly realise is that, somewhat annoyingly, we very often have to shoehorn data into a datatype because the datatype we want to use isn’t available in the format that is used. Perhaps the most common example of this is timestamps: In JSON, you usually put it into a string in a predefined out-of-band format (ISO 8601).

There are subtler ways to emit data out-of-band than timestamps though. One of them is the collection types we shoehorn our data into. It’s subtle because we usually don’t even realise that we shoehorn them into these collection types: I believe that most of the time, it’s because the programming languages we use don’t have the collection types that really fits our data easily available. As a result, we tend to not even consider them as an option. There may be other reasons, and I’ll describe them some sections further down.

As an example of this problem, consider a JSON API endpoint for our favourite fictional issue tracking system, which – among other things – returns all the labels we have attached to an issue:

{
  // ...
  "labels": ["bug", "blocker", "sql-related"],
  //...
}

If we don’t know anything about our issue tracking system, the only thing we may infer from this information is that there might be multiple labels placed on a ticket. But is it possible to have multiple "bug" labels on a single issue? And does it mean anything that "bug" is the first element in the label list, or is that just a coincidence?

Of course, if we read the documentation, we notice that the labels form a set, so order does not matter and we cannot have the same label attached multiple times to a single issue.

But this information is out-of-band. And while it may be worthwhile to have information out-of-band every now and then, I believe we should at least attempt to minimise it as much as possible ¹. Rich Hickey has already explained why out-of-band usually is bad in his talk Language of the System, but let’s touch on why it is bad in this particular instance:

By using a collection type that doesn’t actually represent the collection type we actually transmit, we either have to manually convert it into the real collection type after we’ve decoded the data, or know a priori that the functions we call with this data doesn’t use properties of the collection type that this collection doesn’t have. In short, by shoehorning our data into collection types with different semantics, we add incidental complexity to our system.

Using the right collection type is one thing, but another is to use simpler² alternatives whenever possible. As such, it is interesting to think about simpler collections in general. The first question that may pop to mind is: Are sets simpler than lists? It seems plausible, as sets have no ordering and no duplicates.

But it is also interesting to take it a step further and think about what the simplest collection type is. And is this collection useful for anything?

Lists

It’s tempting to pick the most basic list implementation and call it the simplest data structure: The singly linked list. Through cons, car/first and cdr/rest, we can build up all the functions we need for list manipulation. The ones that immediately pop to mind are size, reverse and map, but there are tons of other useful functions out there.

Implementation wise, you probably can’t get smaller than this. But as a user of a data structure, this is certainly not the simplest data structure. It’s not that hard to see why: A list imposes an ordering on the elements it contains. But when you want to model groups of people, like a school class or all the collaborators on the Rust programming language, then there is very rarely a need to order them from the get-go. Sure, it is handy to have a list of pupils sorted on their name, but that’s incidental, and something we can do later down the pipeline, or as an index in the database. We don’t need any ordering to compute the class’ average grade, for instance.

It’s perhaps easier to see why if we consider these as SQL statements. Without an ordering, we have the straightforward

SELECT the, fields, i, want
FROM pupils;

which, depending on what you want to do, may be sufficient for your needs. If you want ensure that the result is ordered by names, though, you would have to write

SELECT the, fields, i, want
FROM pupils
ORDER BY lastname ASC,
         firstname ASC;

So why do we treat them as the same? It certainly makes sense to do rows.get(i) on the latter, but not on the former which has no ordering. Maybe sets are more useful in those situations?

Sets

Efficient sets are certainly way more complex from an implementation standpoint, but from a user’s perspective, they aren’t necessarily more complex to use. Given just two operations, insert, and fold, we have the bare minimum for a usable set implementation. fold can be considered as an implementation of foldl/reduce, but without any guarantee on order.

To illustrate usage, let’s play around with it in pseudo-Clojure:

(defn set-map
  [f s]
  (fold (fn [s' v] (insert s' (f v))) #{} s))
;; #{} is the empty set

(defn set-sum [s]
  (fold + 0 s))

(let [myset #{1 2 3}]
  (set-sum (set-map inc myset)))
;; => 9

But are sets simpler than lists? As they have no ordering, one might be tempted to say yes. It’s unfortunately not that straightforward though.

Equality

As we all know, a set will not have any duplicates. We can translate “no duplicates” into “For all pairs (e1, e2) in a set, e1 is a “different” element than e2, e1 != e2“. A set implementation, therefore, depends on some definition of =, something an implementation of a list doesn’t.

Equality is not always easy to define. For example, it is always the case that the Java regular expressions "a+" and "aa*" are not equal, although they match the exact same strings. And even if they are based on the same string, they will not be equal unless it is the exact same object: (= #"a+" #"a+") returns false.

Another cause of confusion is the fact that you can have different definitions of equality. In Clojure, (= 1 1.0) returns false, but (== 1 1.0) (numeric equality) returns true. But Clojure’s set implementation will only use = for equality, and so if we wanted to use numeric equality instead, we’d have to wrap the numbers in a new class redefining .equals.

Compared to other languages, Clojure is not that bad. In Common Lisp, you have no less than 4 different equality functions: eq, eql, equal and equalp. And OCaml has its own can of worms with its polymorphic compare. As such, sets may not be as simple as we initially assumed they might be.

No Duplicates?

It also turns out that “only one of each value” is not always what we want. If we go back to our example with our school class, assume we want to calculate the average grade for a specific subject. We can do it like this with our set implementation:

(defn set-count [s]
  (fold (fn [c _] (inc c)) 0 s))

(defn average-grade [subject class]
  (/ (fold (fn [sum pupil]
             (+ sum (get-in pupil [subject :grade])))
           0
           class)
     (set-count class)))

(average-grade :math my-class)
;; => 3.1

But we can’t do it in this fashion:

(defn average-grade [subject class]
  (/ (set-sum
       (set-map #(get-in % [subject :grade])
                class))
     (set-count class)))

because set-map would filter out duplicates – certainly a bad thing!

This is annoying from a simplicity standpoint. Although the latter is incorrect, it is certainly more readable: The grade extraction and summation is decoupled, and would by definition be simpler if it was working the way we wanted it to.

So although sets have no ordering, we cannot always use them for things where we may end up with duplicates. Lists can be a replacement, but they have unnecessary ordering for many purposes.

Order or Equality, Pick None

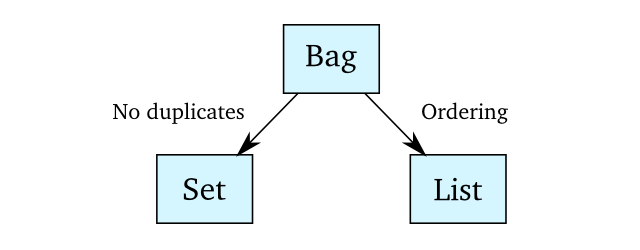
Lists and sets seem like simple collection types, but they enforce either order or depend on equality. As seen in the previous example, there are cases where you need duplicates but do not need ordering.

When we remove the duplicate constraint in sets, or “hide” the ordering in a list, you end up with the same data structure: The bag. This illustration shows how they relate:

So, what operations can you do on a bag? As with sets, you can do two things on them: insert and fold. There is no possibility to look up values in a bag, as the bag doesn’t know about equality.

Most of us actually interact with bags all the time, although we don’t usually realise it because they are often coerced into ordered collections. If we peek into PostgreSQL’s documentation on the SELECT statement, for example, you can read the following two sentences:

If the ORDER BY clause is specified, the returned rows are sorted in the specified order. If ORDER BY is not given, the rows are returned in whatever order the system finds fastest to produce.

Therefore, unless you always know what the fastest result is, you should treat select statements without an ORDER BY clause as a bag – they have no ordering you could safely rely on³.

Following the average grade example we used earlier, we can now use it with the bag:

(defn bag-count [b]
  (fold (fn [c _] (inc c)) 0 b))

(defn bag-sum [b]
  (fold + 0 b))

(defn bag-map [f b]
  (fold (fn [b' v] (insert b' (f v))) #[] b))
;; #[] is the empty bag

(defn average-grade [subject class]
  (/ (bag-sum
       (bag-map #(get-in % [subject :grade])
                class))
     (bag-count class)))

Just a List

The “naïve” implementation of a bag is very straightforward: Just use any (persistent) list – the persistent vector or a lazy seq will do just fine. The only thing you have to ensure is that you only expose the two functions fold and insert and nothing else. This is interesting, as you have to strip off functionality to get the desired interface.

Equality is Sort of a Big Deal

We can do everything we need to do using only fold and insert, but it’s usually handy to have other functions available. Like with the set implementation, we don’t have any remove function, although those could easily be implemented:

(defn set-remove [s elem]
  (fold (fn [s' v] (if (= elem v) s'
                       (insert s' v)))
    #{} s))

(defn bag-remove [s elem]
  (fold (fn [[removed? s'] v]
          (if (and (not removed?) (= elem v))
             [true s']
             [removed? (insert s' v)]))
    [false #[]]
    s))

The bag implementation is a bit hairier, as this implementation of remove only removes one element, not all of them. As such, we have to store a boolean that tells us whether we have removed an element or not.

However, bag-remove introduce =, meaning that we couple the data structure with some definition of equality again. And if the bag implementation is aware of the notion of equality, it must just be as “complex” as a set, it just allows duplicates.

But is a bag with some notion of equality a bag? This is where I struggle to find an established answer: Many mathematicians consider a bag and a multiset to be synonymous, where they define it as a generalisation of a set. The problem is, though, that a multiset has definitions for union, intersection, subset, and so forth. Clearly, all of those depends on a definition of equality.

The bag I was talking about earlier doesn’t know about equality, yet all instances of multiset/bag in papers I have found assume they do. Just to avoid some confusion, when I talk about a multiset, I assume it knows about equality. A bag does not.

Performance and Multisets

Although the pure bag may be simpler implementation wise, it’s not always the right choice. Multisets are at times more manageable, and usually, some notion of equality isn’t that hard to provide. In fact, on some platforms, some notion of equality is provided by default – the JVM .equals and OCaml’s built-in polymorphic compare being the two examples I’ve run with.

It would probably be a stretch to assume that our class and average grade example couldn’t fit in memory, so a better example is perhaps the WordCount example for MapReduce in the Hadoop tutorial: You’re asked to find the word frequency in a gigantic input set – and want to optimise it by running it on multiple machines.

Internally, multiset implementations are usually just a nice wrapper around frequency maps: A value is associated with the times it has been inserted in the map. If the number ever reaches zero, the value is removed from the map. So for our purposes, word counting, this is easily done.

A multiset usually provides a lot of efficient functions to manipulate them like sets. In this example, we only need insert, fold, merge and frequencies. frequencies just return the internal frequency map – perhaps better known as multiplicities in mathematics, but as Clojure ships with frequencies, it makes sense to “reuse” the name.

(defn count-words [input]
  (let [words (split-on-words input)]
    (fold insert empty-multiset words)))

(defn process-work [all-input]
  (let [chunks (split-input all-input)
        partial-results (send-off-work count-words chunks)]
    (frequencies
      (fold merge empty-multiset partial-results))))

Since we don’t particularly care about order, the words and partial-results may be lazy bags of values. They could be anything that can be folded and does not remove duplicates, though.

Now With More Functions

“It is better to have 100 functions operate on one data structure than 10 functions on 10 data structures.” – Alan Perlis

Of course, if you ever were to add or use bags and multisets in a language, you would want more functions than just insert and fold. They should compose well with the other data structures, and preferably be drop-in replacements in cases where ordering isn’t used.

That’s not extremely problematic to do in Clojure/ClojureScript. You just have to figure out what interfaces/protocols the other implementations extend, and pick the ones relevant for bags:

user=> (ancestors (type #{}))
;; List of ancestors

user=> (ancestors (type []))
;; ...

So you could make this work without too much hassle, at least in Clojure. Other languages may or may not make this as easy.

And the Rest of the World?

It is entirely possible to make good and useful implementations of bags and multisets, but would people use them? Well, bags are just a tiny wrapper on top of a persistent vector/lazy seq that removes functionality and give no performance benefits. Ask anyone if this makes sense, and you’ll most likely get a clear no. Bags as a data structure is a hard sell because it looks like they have no value.

Is it a problem that we use lists where we really should use bags? I don’t think it would cause great harm, but it might give users of APIs unexpected assumptions. As we saw earlier, select queries in SQL have no ordering unless ORDER BY is provided. You can bet that, if you reversed the order SQL databases gave you unordered output, a lot of programs will end up with unintended behaviour. Although the documentation gives you this information, it’s easy to skip or not notice properly.

My guess is that this specific problem is bigger for sets. The fact that most data serialisation formats⁴ don’t have any set definition makes it easy to make sets as lists. Now, consumers of the data source are responsible for converting it/treating it as a set – with everything that entails. I could probably find a ton of examples of this problem, roles in CouchDB being just one example of this I recently noticed. (Bonus points if you can figure out if you can have duplicates or if ordering matters in the documentation.)

Using lists instead of sets is certainly not the biggest issue out there in the world – we shoehorn data into many other types of data formats that is way more problematic. And I’m in no way arguing that we should just use this new data format X which supports all these things, because we all know how well introducing new standards go.

But if you ever consider making a new data serialisation format, and somehow the XKCD above doesn’t apply, consider what data collections you bring in. Bags and sets may make it easier for consumers of the format to create sensible and more evident APIs, because we now know whether duplicates are allowed and if the ordering is important. As an additional bonus, users of your format may end up with less incidental complexity in their systems⁵.

And if you need to decide on a data format, and you are reasonably free to pick one, consider transit or EDN, or any other format that supports sets/bags or gives you the option to add that information in-band.